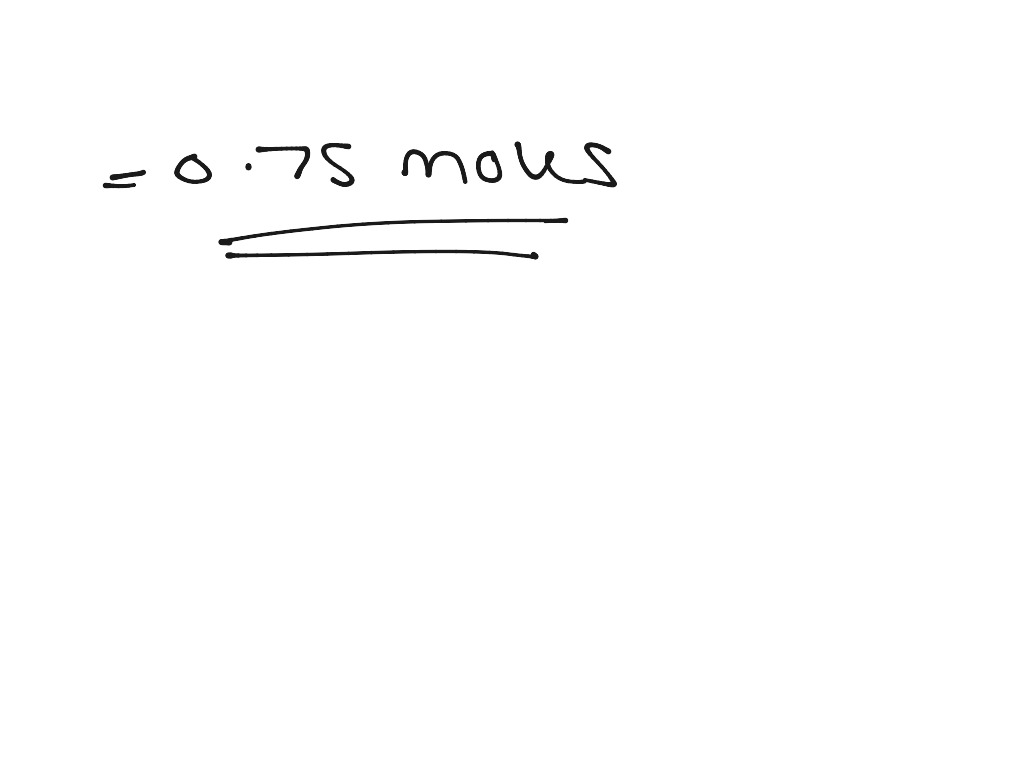Volume is an amount of space, in three dimensions, that a sample of matter occupies. The number and the phase of the molecules in the sample primarily determine the volume of a substance. Volume will be measured in many ways in this course, but the units are usually milliliters or cubic centimeters . Methods for determining or delivering precise volumes include volumetric pipets and pycnometers; less precise methods include burets, graduated cylinders, and graduated pipets. Explain to students that learning to measure volumes takes practice.
Today they will practice measuring different liquids. They will use a container called a graduated cylinder to measure liquids. Graduated cylinders have numbers on the side that help you determine the volume. Volume is measured in units called liters or fractions of liters called milliliters . Students need to follow the directions on the lab sheet carefully.
Remind them that you will be checking how they measure as you move about the room. Some chemistry glassware, called volumetric glassware, is inscribed with markings to make measuring the volume of liquids easier. The pieces of volumetric glassware found in the chemistry laboratory are beakers, Erlenmeyer flasks, graduated cylinders, pipets, burets and volumetric flasks. The density of a substance can be used to define the substance.Water is unusual because when water freezes, its solid form is less dense than liquid water, and thus floats on top of liquid water. In this lesson, students will cooperatively measure the mass and volume of three different-colored crayons as a solid.
After recording measurements, students will place their crayons in molds in order to change the state of matter from a solid to a liquid through heating. The teacher will pour the liquefied crayon into a graduated cylinder to measure the volume. Following the measurements recording, the liquid will be poured back into the molds and placed in a cool/shaded environment so the crayons will change back into a solid state. Once the crayons re-solidify, the students will take their student-made, tie-dye crayon out of the mold and re-measure it. Lastly, the students will measure and compare their final measurements to the initial measurements. Because gases fill their containers, their volume is the same as the internal volume of the container.
Liquids are commonly measured using containers, where the volume is marked or else is the internal shape of the container. Examples of instruments used to measure liquid volume include measuring cups, graduated cylinders, flasks, and beakers. There are formulas for calculating the volume of regular solid shapes. Another method of determining the volume of a solid is to measure how much liquid it displaces.
Displacement is usually the method that is used to measure the volume of an irregularly shaped object. The object is simply submerged in a liquid and the volume of liquid that is displaced is measured. As an example imagine a 100 ml graduated cylinder with 50 ml of water in it . In this lesson, students will estimate water volume in three containers and record observations. Following estimations, students will directly measure the volumes using an appropriate method.
After comparing those measurements to the estimates, students will be given a known volume of water and will be asked to divide the water into three predetermined volumes, again using estimation skills. A following measurement will be used to determine the difference between their volume estimate and the actual measured volume as distributed across three vessels. Students will learn how to use a graduated cylinder to make observations based on the volume of liquids. Students will solve word problems based on volume and measure out given liquid volumes. This lesson could also be taught using mathematics instructional time. Students will make learn how to find the volume of irregular objects using a graduated cylinder.
Students will solve problems based on the volume of irregular objects and determine the volumes of given objects. What are some reasons that groups might have different values for density? Students should realize that small inaccuracies in measuring volume can account for differences in density values. Another reason is that the graduated cylinder, itself, is not perfect. Remind students that in the beginning of the lesson they made a prediction about the density of the small, medium, and long sample. Students should have predicted that the longest cylinder has the lowest density, the shortest cylinder has the highest density, and the middle is somewhere in between.
To use the water displacement method, an object is inserted into a graduated cylinder partially filled with water. The object's volume occupies space, displacing liquid and raising the water level. The difference between the two volumes, before and after the object was inserted, is the object's volume. Measure the volume of liquids and solids using beakers, graduated cylinders, overflow cups, and rulers. Water can be poured from one container to another and objects can be added to containers.
A pipette can be used to transfer small amounts of water, and a magnifier can be used to observe the meniscus in a graduated cylinder. Test your volume-measurement skills in the "Practice" mode of the Gizmo. Scientists who work in a laboratory must be familiar with typical laboratory glassware, often called volumetric glassware. These may include beakers, a volumetric flask, an Erlenmeyer flask, and a graduated cylinder. Each of these containers is used in a laboratory setting to measure liquid volumes for different purposes. We can measure the area of irregular bodies by using graph paper.
But it is impossible to measure the volume of irregular bodies by using graph paper. We can measure the volume of irregular bodies by using measuring cylinder. This method is based on the fact that the volume of an irregular solid is equal to the volume of water displaced by it when it is immersed in water. When we immerse an irregular body in water, it displaces some amount of water. The volume of displaced water is equal to the volume of an irregular body that displace water. This method can be used to calculate the volume of those irregular bodies which sink in water and do not dissolve in water.
The accuracy of the markings on volumetric glassware varies greatly. The markings on beakers and flasks are usually about plus or minus 5% of the volume of the container. As such, they should be used only when a rough estimate of volume is required. Volumetric flasks, burets and pipets are the most accurate with tolerances of less than 0.2%. To achieve these accuracies the person using the device needs to use the proper technique and the measurements need to made at the temperature for which the glassware was calibrated .
Measuring the volume of irregularly shaped objects by immersion can be an idea for a science project in the area of physical science or physics. The biggest problem is in verifying that your results are correct. You could establish an empirical rule using known volumes before using the method on unknown volumes. Similar to beakers, graduated cylinders are tall, cylindrical containers with a spout for pouring. They have hash marks on the side to measure the volume of a liquid. Most labs have graduated cylinders in a variety of sizes.
Typical volume measurements are 10 mL, 25 mL, 50 mL,100 mL, 500 mL and 1,000 mL. Although the two terms often are used interchangeably, there is a technical difference between specific gravity and density. Density is defined as the mass per unit volume of a substance. When the specific gravity is defined based on water at 4°C, then the specific gravity is equal to the density of the liquid.
However, if the specific gravity is expressed at different temperatures, it will no longer be equal to the density. Although there is a difference between specific gravity and density, for the most part the values are similar enough to be used interchangeably in most situations. In science, length may be measured with a metric ruler using SI units such as millimeters and centimeters.
Scientists measure mass with a balance, such as a triple beam balance or electronic balance. In science, the volume of a liquid might be measured with a graduated cylinder. In this SaM-1 Video, students will learn how to find the volume of irregular objects using a graduated cylinder and the displacement method. Use a graduated cylinder and water to accomplish this task.
Volumetric labware is for measuring liquids with precision. Volumetric flasks, burettes, and pipettes made for measuring small amounts of liquid are the most accurate, with tolerances of less than ±0.02. Research and testing require precise measurements, and many lab vessels are even designed to account for the liquid residue that clings inside a flask. Therefore, scientists can be confident that the measurements poured out of volumetric glassware are precise and accurate. Litre, fluid ounce, gallon, quart, pint, tsp, fluid dram, in3, yd3, barrelIn SI base units1m3DimensionL3Volume is a scalar quantity expressing the amount of three-dimensional space enclosed by a closed surface. For example, the space that a substance or 3D shape occupies or contains.
Volume is often quantified numerically using the SI derived unit, the cubic metre. Volumes of some simple shapes, such as regular, straight-edged, and circular shapes can be easily calculated using arithmetic formulas. Volumes of complicated shapes can be calculated with integral calculus if a formula exists for the shape's boundary. One-dimensional figures and two-dimensional shapes are assigned zero volume in the three-dimensional space. Calculate the uncertainty in the mass of water removed using error propagation. Convert this mass to volume units by dividing by the density of water (use a precise value, specific to the water's temperature).
This value equals the uncertainity in the volume of the metal cylinder. For less defined shapes, volume can be determined by water displacement. Volumes of liquids such as water can be readily measured in a graduated cylinder. The discussion focusses on the relationship between particle size, shape, and the VSSA, followed by an overview of instrumentation, experimental methods, and standards. Off-the-shelf calorimeters are typically used for hydrocarbon-based fuels and not designed for simulating metal powder oxidation in gaseous environments.
We have developed a method allowing a typical bomb calorimeter to accurately measure heat released during combustion and achieve nearly 100% of the reference heat of combustion from powder fuels such as aluminum. The modification uses a combustible organic dispersant to suspend the fuel particles and promote more complete combustion. The dispersant is a highly porous organic starch-based material (i.e. packing peanut) and allows the powder to burn as discrete particles thereby simulating dust-type combustion environments. The demonstrated closeness of measured Al heat of combustion to its reference value is evidence of complete metal combustion achieved in our experiment.
The rate of heat release is an important additional parameter characterizing the combustion process. A technique for measuring effective conductivity of conductor materials using 3D printed re-entrant cavity resonator is proposed. An analytical formula for the extraction of the effective conductivity has been derived in relation to energy stored in the volume of the cavity geometry. A method of resonant cavity characterisation of material based on microwave losses is utilised for the measurements. The approach offers a simplified analytical method and also supports the measurements of sample with arbitrary thickness.
Samples produced from three different manufacturing processes of computer numerical control and 3D printing, made of aluminium, copper and stainless steel were measured to demonstrate the method. The 3D printed and copper coated polymer sample is considered as reference material for the measurements. The measured results have shown that the copper coated polymer sample have similar conductivity with that CNC copper. This signifies the good finishing, low surface roughness and quality of copper coating used in 3D printed polymer device. In-situ monitoring is an important aspect of geotechnical projects to ensure safety and optimise design measures. However, existing conventional monitoring instruments are limited in their accuracy, durability, complex and high cost of installation and requirement for ongoing real time measurement.
Advancements in sensing technology in recent years have created a unique prospect for geotechnical monitoring to overcome some of those limitations. For this reason, micro-electro-mechanical system technology has gained popularity for geotechnical monitoring. MEMS devices combine both mechanical and electrical components to convert environment system stimuli to electrical signals. MEMS-based sensors provide advantages to traditional sensors in that they are millimetre to micron sized and sufficiently inexpensive to be ubiquitously distributed within an environment or structure.
This ensures that the monitoring of the in-situ system goes beyond discrete point data but provides an accurate assessment of the entire structures response. The capability to operate with wireless technology makes MEMS microsensors even more desirable in geotechnical monitoring where dynamic changes in heterogeneous materials at great depth and over large areas are expected. Many of these locations are remote or hazardous to access directly and are thus a target for MEMS development. Firstly, experiments were designed to collect the vibration acceleration signals of a UAV working at high speed under three states . Then, considering the powerful feature extraction and complex data analysis abilities of 1D-CNN, an effective deep learning model for fault identification is established utilizing 1D-CNN. And it is also verified that the reconstructed sample set can easily reflect the global information of mechanical operation.
The results show that the 1D-CNN deep learning model could diagnose and identify UAV rotor damage faults accurately, by incorporating the proposed method of interval sampling reconstruction. We will discuss here about the methods of measurement of volume of a substance. It takes the shape of the container in which it is kept.
So we cannot measure liquid with a measuring tape or a scale. But we can measure the volume of a liquid very easily. In this lesson students will investigate what mass and volume are and how they are measured. Students will practice measuring the masses of solids and volumes of liquids.
Students will have a chance to work cooperatively with their peers and apply their knowledge to a real-world problem. The accuracy of the markings on laboratory glassware varies. Larger containers, like beakers and flasks, are typically ±5% of the total volume. They are generally used only when the volume measurement does not need to be precise. For graduated cylinders, the margin of error, or tolerance, is about 1%. Liquid volume – Measure liquid volume using calibrated containers.
Often, the volume obtained by mixing liquids is additive, but this is not always the case. The volume of miscible liquids may be less than the sum of the separate volumes. Also, dissolving solids into liquids doesn't always result in additive volume. To perform pycnometry measurements, the mass of the cylinder and the mass of a flask filled with water to a mark (A, Fig. 3) are recorded. The volume of water displaced is removed by pipet, thereby restoring the water level to the mark .
The combined mass of the flask, remaining water, and cylinder is then measured. At first for the measurement of the volume of liquids, the liquid is poured into the measuring cylinder, then the volume of the liquid is calculated by observing the reading given on the surface of the cylinder. What do you do with an irregular object, though, such as a pen or a rock? The Greek philosopher Archimedes was faced with this problem when he was asked to find the density of the king's crown. To determine its density, he had to know its volume, and his "Eureka" moment occurred when he realized he could do it by immersing the crown in water and measuring the amount of water that was displaced. The displacement method is still the standard way to determine the volume of an irregularly shaped object.
Rolling bearing is a widely used component in engineering. Fault diagnosis of rolling bearing is the key issue to ensure the normal operation of equipment. At present, the research on fault diagnosis of rolling bearing mainly focuses on the analysis of vibration data under constant working conditions. Nevertheless, when dealing with practical engineering problems, the operation of equipment is frequent in the case of variable speed. To analyze the vibration data in the case of frequency conversion and accurately extract the fault characteristic frequency is a challenge especially when the fault characteristics are weak.